Cara Mencari Nilai Perbandingan Trigonometri Sudut Istimewa
Monday, 28 March 2016
Edit
Untuk lebih mudah memahami cara mencari nilai perbandingan trigonmetri pada sudut istimewa (30°, 45° dan 60°), terlebih dahulu harus paham dengan perbandingan trigonometri pada segitiga siku-siku khsusnya definisi sinus, cosinus dan tangen suatu sudut. Selain itu Anda juga harus paham dengan teorema pythagoras. Oke langsung saja pada pembahasannya, sekarang perhatikan gambar berikut.

Gambar di atas merupakan gambar segitiga sama sisi dengan besarnya masing-masing sudut adalah 60°. Pada ΔABC tersebut ditarik sebuah garis dari titik C menuju titik D yang tegak lurus dengan garis AB, sehingga membagi sudut ACB menjadi dua bagian yang besarnya sama yakni 30°. Misalkan panjang AD = BD = x, maka panjang AC = BC = 2x. Dengan menggunakan teorema pythagoras maka panjang CD dapat dicari yakni:
AC2 = AD2 + CD2
CD2 = AC2 – AD2
CD2 = (2x)2 – x2
CD2 = 4x2 – x2
CD2 = 3x2
CD = √(3x2)
CD = x√3
Sekarang kita cari nilai perbandingan trigonometri pada segitiga siku-siku ACD pada sudut 30°, yakni:
sin 30° = AD/AC = x/2x = ½
cos 30° = CD/AC = x√3/2x = ½√3
tan 30° = AD/CD = x/x√3 = (1/3)√3
Sekarang kita cari nilai perbandingan trigonometri pada segitiga siku-siku ACD pada sudut 60°, yakni:
sin 60° = CD/AC = x√3/2x = ½√3
cos 60° = AD/AC = x/2x = ½
tan 60° = CD/AD = √3x/x = √3
Bagaimana dengan perbandingan trigonometri pada sudut 45°? Silahkan perhatikan gambar segitiga siku-siku di bawah ini.

Perhatikan segitiga ABC di atas dengan siku-siku berada di titik A. Sudut A = 90°, sudut B = C = 45°. Jika panjang AB = AC = x maka dengan teorema pythagoras kita bisa cari panjang BC yakni:
BC2 = AB2 + AC2
BC2 = x2 + x2
BC2 = 2x2
BC = x√2
Sekarang kita cari perbandingan trigonometri pada sudut 45°, yakni:
sin 45° = AC/BC = x/x√2 = ½√2
cos 30° = AB/BC = x/x√2 = ½√2
tan 30° = AC/AB = x/x = 1
Berdasarkan penjelasan diatas maka dapat disimpulkan bahwa besarnya nilai perbadingan trigonometri pada sudut istimewa (30°, 45°, dan 60°) terlihat seperti tabel di bawah ini.
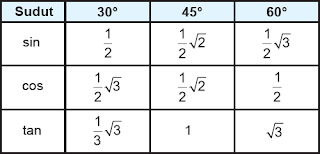
Demikian pembahasan cara mencari nilai perbadingan trigonometri pada sudut istimewa (30°, 45°, dan 60°).